■波長板とは
波長板とは、偏光を制御、分析、および最適化するために不可欠なツールです。 主にレーザ光源に対して、波長の分離、微調整、楕円率の調整、偏光の回転などの目的で使用され、レーザを動かすことなく小さなスペースで作業を実行できるという利点があります。 また、高パルスや連続発振(CW)のレーザにも適用することができるので、自由度が高く、低価格で構成を組むことが可能です。
波長板の種類には、一般的によく使用されるものとして、直線偏光の偏光方向を回転させる1/2波長板、直線偏光を円偏光に変換する1/4波長板があります。他にも、1波長板または鋭敏色板と呼ばれる干渉色を得る目的で使用されるものや、直線偏光を楕円偏光に変換する1/8波長板など、用途に合わせて多種多様な波長板が存在しています。
■波長板の用途
波長板の用途としては、レーザの偏光方向を変えたり光量を可変させるという使い方をはじめ、複屈折結晶やファラデー回転子と共に使用することで光アイソレータとして、ファラデー回転子や偏光ビームスプリッタや反射ミラーと共に使用することで光サーキュレータとして、たくさん並べて使用することで偏光スクランブラとしてよく使用されています。その他以下のような用途で使用されています。
- レーザー : 波長を組み合わせたり分断したりすることで、Qスイッチングにより非常に高いパルスパワーが達成され、破壊的なフィードバックを起こらなくさせます。
- 加工用レーザ : 円偏光でよりきれいで均一な切断が行えます。
- 医療や工業用の多軸ビーム照射システム : 偏光制御によって電力損失と変動が最小限に抑えられます。
- 光通信 : 波長分割多重方式(WDM)において、光ファイバで送られた多数の波長は、波長板を組み込んだ装置によって多重化され経路が指定されます。
- 顕微鏡 : サブ波長の高さの特徴を生かし、鮮やかな色で表示することができます。
- 生物学や鉱物学 : 波長板によって区別された異なる色の偏光に対する作用を利用して、標本を分析できます。
- 醸造 : 偏光回転の程度によって糖度を測定することができます。
- 距離計 : 強い出力パルスと弱い戻り光を分断します。
以上はほんの一部の例でしかなく、他にもさまざまな用途で使用されており、新しい用途としての研究も進んでいます。
■波長板の動作原理
波長板は、光波の2つの垂直偏光成分間の位相をずらすことによって機能します。典型的な波長板は、用途に合わせて光軸の向きと厚さが決定された複屈折結晶です。結晶の光軸が板の表面と平行になるように結晶の方向を選択して、結晶を板に切断すると、切断面内に2つの軸、屈折率がnoの常軸と屈折率がneの異常軸が得られます。通常の軸は光軸に垂直です。異常軸は光軸と平行です。プレートに垂直に入射する光波の場合、常軸に沿った偏光成分は速度vo = c/noで結晶を通って進み、一方、異常軸に沿った偏光成分は速度ve = c/neで移動します。これによって、それらが結晶を出るときに2つの成分間に位相差をもたらします。方解石のようにne < noの場合、異常軸は速軸と呼ばれ、常軸は遅軸と呼ばれます。 ne > noの場合、速軸と遅軸は逆になります。(図1.参照)
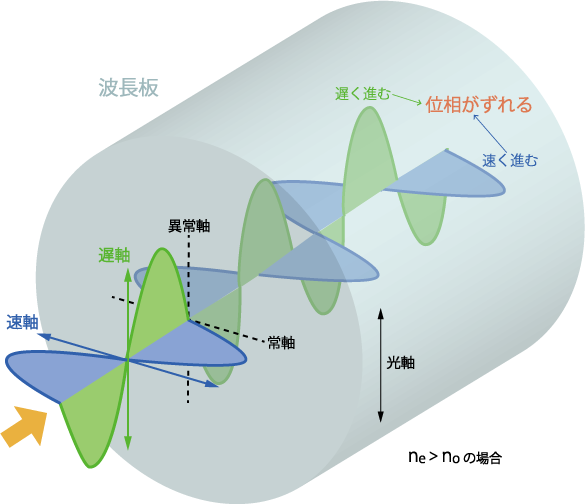
図1. 波長板における位相差のメカニズム
結晶の厚さに応じて、両方の軸に沿って偏光成分を有する光は異なる偏光状態で現れます。波長板は、それが2つの成分に与える相対位相の量Γによって特徴付けられ、これは次式によって複屈折Δnおよび結晶の厚さLに関係付けられます。
\[\Gamma = \frac{2\pi \Delta n L}{λ_0}\]
ここで、λ0は光の真空波長です。
■1/2波長板
1/2波長板は、入射光の2つの垂直偏光成分間にπ(=λ/2)の位相差を与えて出射させる波長板です。(図2.参照)
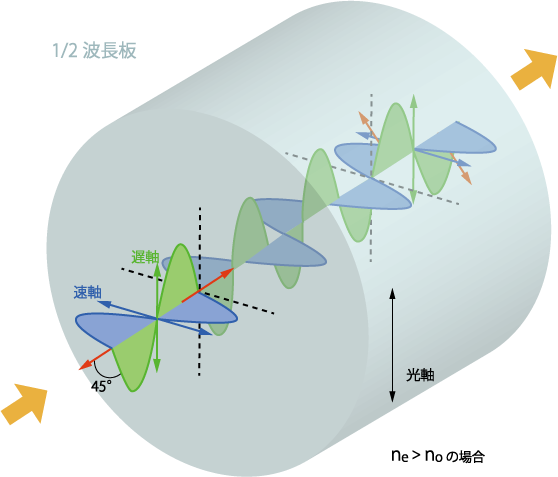
図2.1/2波長板による偏光方向を変えるメカニズム
入射光の偏光方向(赤色矢印)が、波長板の速軸(または遅軸)に対してθの方位角で入射した場合、その偏光方向を2xθ回転させて出射することができます。すなわち45°の方位角で入射したときの90°が最大の回転角になります。
このことを数式で示すと以下のようになります。
入射光の成分を、偏光方向(赤色矢印):ベクトルp、速軸(青色矢印):ベクトルf、遅軸(緑色矢印):ベクトルs、ベクトルpとベクトルfの間の角をθ、波の伝搬軸(黄色矢印):zとすると、入射光の電場は、
\[E \mathrm{e}^{i(kz-\omega t)} = E\vec{p}\mathrm{e}^{i(kz-\omega t)} = E(\cos \theta \vec{f} + \sin \theta \vec{s})\mathrm{e}^{i(kz-\omega t)}\]
と表せます。
1/2波長板では、入射してから出射するまでに波のf成分とs成分との間にe^(iΓ) = e^(iπ) = -1の位相差を与えるので、この値を導入すると出射光の電場は、
\[E(\cos \theta \vec{f} – \sin \theta \vec{s})\mathrm{e}^{i(kz-\omega t)} = E\{\cos (-\theta) \vec{f} + \sin (-\theta) \vec{s}\}\mathrm{e}^{i(kz-\omega t)}\]
と表せます。
出射光の偏光方向をベクトルp’、出射光の速軸をベクトルf’とすると、その間の角は-θとなり、入射光と比べると偏光方向が2θ回転された状態で出射されたことになります。
後に解説することに触れますが、入射光の偏光成分が円偏光や楕円偏光の場合、1/2波長板を通すことによってその向きを逆にすることができます。
■1/4波長板
1/4波長板は、入射光の2つの垂直偏光成分間にπ/2(=λ/4)の位相差を与えて出射させる波長板です。(図3.参照)
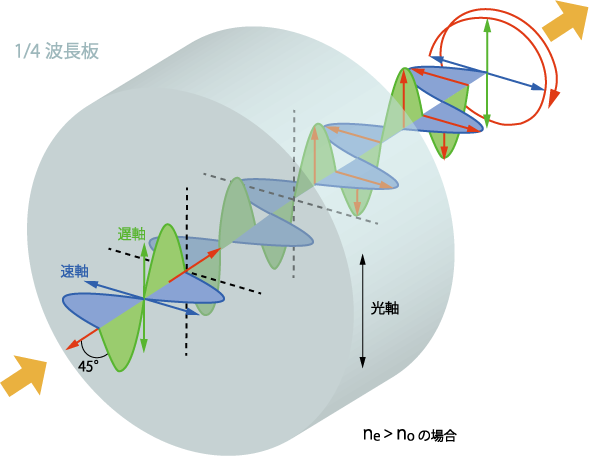
図3.1/4波長板による直線偏光を円偏光に変えるメカニズム
入射光の偏光方向(赤色矢印)が、波長板の速軸(または遅軸)に対して45°以外の方位角で入射した場合、出射光は楕円偏光になり、45°の方位角で入射した場合は円偏光になります。
このことを数式で示すと以下のようになります。
入射光の成分を、速軸(青色矢印):ベクトルf、遅軸(緑色矢印):ベクトルs、波の伝搬軸(黄色矢印):z、EfとEsを実数とすると、入射光の波は、
\[(E_f \vec{f} + E_s \vec{s})\mathrm{e}^{i(kz-\omega t)}\]
と表せます。
1/4波長板では、入射してから出射するまでに波のf成分とs成分との間にe^(iΓ) = e^(iπ/2) = iの位相差を与えるので、この値を導入すると出射光の波は、
\[(E_f \vec{f} + i E_s \vec{s})\mathrm{e}^{i(kz-\omega t)}\]
と表せます。
この段階では円偏光および楕円偏光を表しますが、入射光の偏光軸が速軸と遅軸に45°をなす場合、Ef = Es ≡ Eとなり出射光の波は、
\[E(\vec{f} + i \vec{s})\mathrm{e}^{i(kz-\omega t)}\]
と表すことができ、円偏光になります。
まとめると、入射光の偏光軸が速軸や遅軸に0°をなす場合、偏光は変化しないので出射光も直線偏光、0°より大きく45°よりも小さい場合は楕円偏光、45°の場合は円偏光になります。また、可逆的に、円偏光や楕円偏光の入射光を直線偏光に変えて出射することができます。
< こちらから関連製品をご覧いただけます >