■光ファイバーの開口数(NA)とは
光ファイバーの開口数(NA:Numerical Aperture)とは、光ファイバに伝搬可能な光(伝搬モード)を入射させる(あるいは、光ファイバから出射する)ことができる最大の入出射角を表します。主にマルチモードファイバで使われ、入射させやすさや伝搬モード数、曲げ損失などを表す指標の一つです。
■光ファイバーの開口数(NA)の定義
光ファイバーの伝搬モードは、コアとクラッドの境界で全反射を繰り返しながら伝搬して行きます。ステップインデックス型光ファイバの場合、端面に入射角θinで入った光線は、コア内でθcoreの角度を持って進み、コア・クラッド境界面には90°-θcoreの角度で到達します(図1.参照)。入射して来た光が、コア・クラッドの境界面に沿って進む(θcladが90°となる)ようになるときの入射角内をθin max、ファイバ外周の媒体の屈折率をn(大気の場合にはn=1となります)とするとき、開口数(NA)は
\[NA = n\sin θ_{in\ max} = \sqrt{{n_{core}}^2 – {n_{clad}}^2}\]
で定義されます。
ここで、n sinθin maxは、以下から導出できます。入射端面では、
\[n\sin θ_{in\ max} = n_{core} \sin θ_{core\ max}\]
コア・クラッド境界面では、
\[n_{core} \sin θ (90^\circ – θ_{core\ max}) =n_{core} \cos θ_{core\ max} = n_{clad} \sin 90^\circ = n_{clad}\]
両式より、
\[n\sin θ_{in\ max} = n_{core} \sqrt{1 – \cos^2 θ_{core\ max}} = n_{core} \sqrt{1 – \frac{{n_{clad}}^2}{{n_{core}}^2}} = \sqrt{{n_{core}}^2 – {n_{clad}}^2}\]
となります。
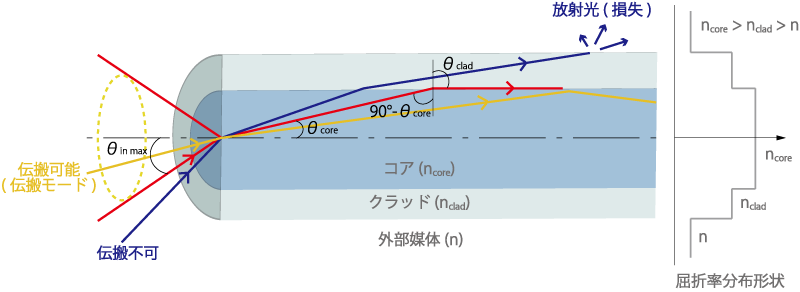
図1. 伝搬可能な光と入射角
n=1である大気中で入射させる場合、NA=θin maxより小さい入射角の光は全反射して伝搬モードとなり、θin maxより大きい入射角の光はクラッドに入り、クラッド内を伝搬しその後最終的にはクラッド外周で散乱して放射(損失)光となります。
光ファイバ中を伝搬していくことができる伝搬モードは、コア・クラッドで全反射する光波すべてではありません。光波の伝搬定数の伝搬軸方向成分が1周期(2π)分伝搬したとき、伝搬軸に垂直な伝搬定数の断面方向の位相変化量も2πの整数倍だけ変化するものだけが、伝搬モードとなります(このような波を定在波といいます)。(図2.参照)
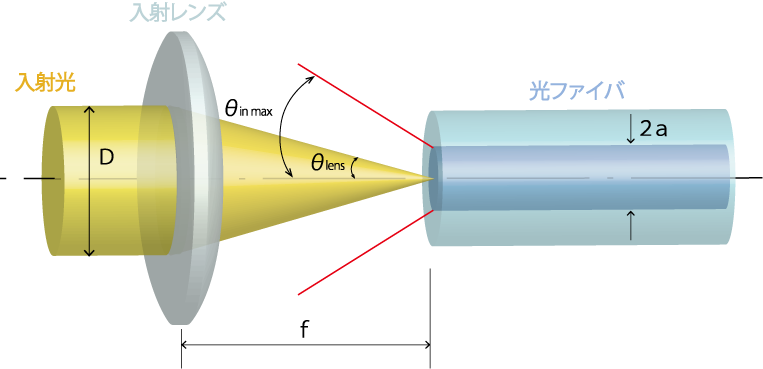
図3. 集光レンズによる光ファイバへの光入射
>
シングルモード光ファイバに効率よく入射させるには、NAよりも焦点におけるビーム径ω0をモードフィールド径(MDF)に合わせる必要があります。
ビーム直径Dの平行光線のレンズの焦点面におけるビーム径ω0は、λを波長として、
\[ω_{0} = \frac{2λf}{\pi D}\]
となります。
■伝搬可能なモード総数
光ファイバーの重要指標である正規化周波数v(=2πa NA/λ)が十分大きな(10程度以上)とき、ステップインデックス型マルチモードファイバの伝搬可能なモード総数(最高次モード番号)Nは、aをコア半径として
\[N \ \approx\ \frac{v^2}{2} = 2(\frac{\pi a {NA}}{λ})^2\]
で近似できます。これから、伝搬可能なモード総数Nは、開口数(NA)の2乗に比例して増えることがわかります。
■開口数(NA)を利用した光ファイバーの曲げ損失の評価
開口数(NA)は光ファイバーの曲げ損失を評価するときにも使われます。光ファイバが曲げ半径rで一様に曲がっているときの曲げ損失αbとNAとの関係は、
\[α_{b}\ \ \propto \ \ \mathrm{e}^{(-\frac{r\sqrt{\Delta^3}B}{λ})}\]
で表されます。ここで、Bは規格化周波数に依存する値、⊿は次式で定義される比屈折率差で、
\[\Delta = \frac{{NA}^2}{2{n_{core}}^2}\]
となりNAの二乗に比例しています。また、ケーブル化などにより生じる微小な不規則曲がりに起因するマイクロベンディング損失αmは、
\[α_{m}\ \ \propto \ \ \overline{(1/R)^2}\ ・ \frac{λ^{2p}}{\Delta^{2p+1}}\]
で表されます。ここで、
\[\overline{(1/R)^2}\]
は微小な不規則曲がりの曲率の二乗平均、pは微小な曲がり(マイクロベンド)の不規則性を表す値です。これらから、曲げ損失αb、αmはNAに強く依存しており、NAが大きくなると損失は共に小さくなることが分かります。